Cabri et les anamorphoses
Chantal Gabriel-Randour and Jean Drabbe
Brussels , Belgium
4. Les peintres mathematiciens
1 Introduction
De janvier à mars 2001, nous avons préparé avec les élèves de 5ème et 6ème années de l’Athénée Royal Gatti de Gamond, une exposition sur le thème Miroirs et Perspectives. Nous nous sommes intéressés à divers aspects du miroir en chimie, en physique, en philosophie, en histoire et en géographie. Pour comprendre l’évolution de la perspective nous avons visité de nombreux musées réels et virtuels et nous avons étudié l’aspect mathématique de la perspective. Nous avons aussi rencontré des perspectives curieuses que nous avons plus spécifiquement étudiées: les anamorphoses. Des planches extraites de l’oeuvre de Jean-François Niceron nous ont amené à regarder des anamorphoses perspectives et ensuite les anamorphoses à miroir. Pour réaliser nos propres images déformées, nous avons allié la géométrie descriptive et le logiciel CabriTM. Le site http://www.ibelgique.com/mathema reprend une partie de ce travail. Les constructions de base en géométrie descriptive ont été développées par Jean Drabbe.
2 La geometrie descriptive
La géometrie descriptive fut développée par Gaspard Monge (1746-1818),
l’un des principaux fondateurs de l’Ecole Normale de Paris et de l’Ecole
Polytechnique. Elle utilise deux plans de projection perpendiculaires entre
eux: un plan vertical et un plan horizontal. Tout point P de l’espace est
déterminé par Pv , sa
projection orthogonale sur le plan vertical et Ph , sa projection orthogonale sur le plan
horizontal. Le rabattement du plan horizontal sur le plan vertical, utilisant
leur intersection comme charnière (ligne
de terre) permet une représentation plane. Il est à noter que l’on trouve
l’emploi des doubles projections dans le De Prospectiva Pingendi (1486) de
Piero della Francesca et l’Underweysung de Dürer (1525).
L’oeuvre de Jean-Francois
Niceron
Jean-François Niceron (1613-1646) est un érudit et un mathématicien de l’ordre des Minimes à Paris.
Il édite en 1638 la Perspective Curieuse qui est l’un des premiers traités consacré à l’étude systématique des anamorphoses.
Il traite entre autres les anamorphoses perspectives et les anamorphoses à miroir.
Il est à noter qu’il fut précédé par des travaux de Vaulezard qui publie en 1630 La perspective cylindrique et conique ou traité des apparences vues par le moyen des miroirs...
|
|
|
|
|
Portrait de Niceron par Michel Lasne (1642) |
|
|
|
|
||
|
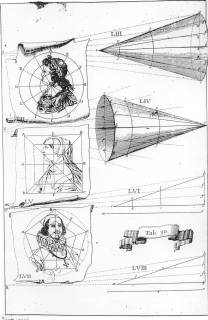
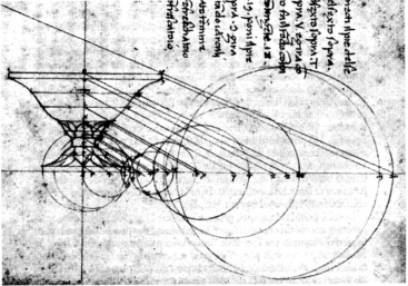
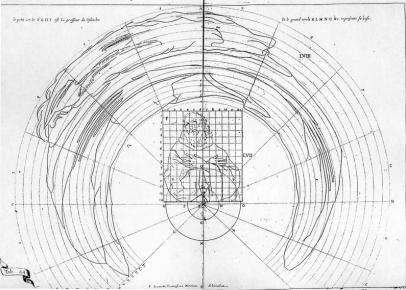
Planche n°30 anamorphoses coniques et pyramidales |
|
La construction legitime et la Renaissance Italienne
Le principe de la perspective dite linéaire, centrale ou artificielle, se développe à Florence au début du XVème siècle.
Les lois de la perspective sont mises en évidence par l’architecte, ingénieur, peintre et sculpteur, Filippo Brunelleschi (1377-1446) et Leon Battista Alberti (1404-1472) architecte et artiste.
En 1436, Alberti achève son traité sur la représentation de l’espace Della Pittura. Il est le premier à énoncer explicitement les règles de la perspective.
|
|
|
|
|
|
|
|
3 La perspective
Le modele mathematique de la perspective
(Extrait du texte de Jean Drabbe)
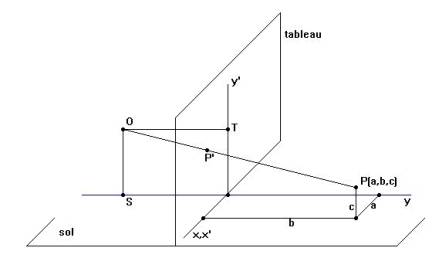
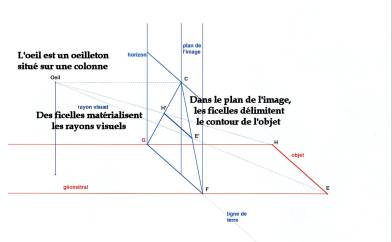
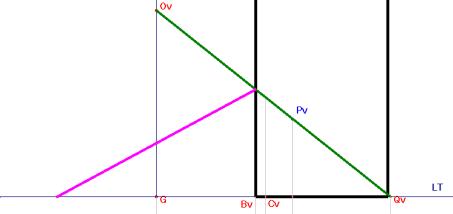
Voici une description du modèle mathématique sous-jacent au dessin en perspective. La toile du peintre est située dans un plan vertical perpendiculaire au plan horizontal du sol. La droite d'intersection de ces deux plans est appelée ligne de terre. Notons O l'oeil du peintre. Chaque point P de la scène est représenté par le point P' intersection du plan du tableau et de la droite joignant O et P.
|
|
|
|
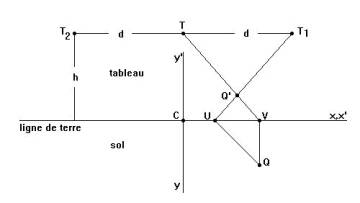
Notons T (resp. S) le pied de la perpendiculaire abaissée de O sur plan du tableau (resp. sur le plan du sol), C le point de percée de la ligne de terre dans le plan déterminé par les points O T S.
Rapportons l'espace au système de coordonnées déterminé par les axes :
Cx sur la ligne de terre ,
Cy est perpendiculaire à la ligne de terre dans le plan du sol ,
Cz est perpendiculaire au plan du sol ;
et rapportons le plan de la toile au système de coordonnées :
Cx' qui coïncide avec Cx ,
Cy' perpendiculaire à Cx' dans le plan du tableau.
Soient d la distance de l'oeil (OT) à la toile et h la hauteur (SO) de l'oeil au-dessus du sol.
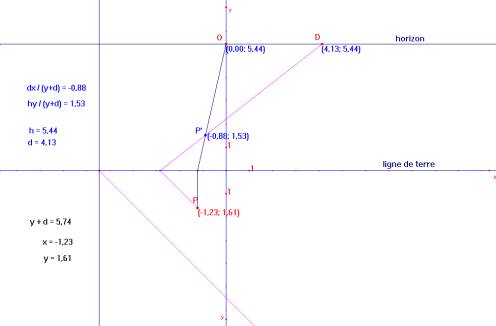
Des propriétés géométriques élementaires (similitude de triangles) permettent d'exprimer analytiquement la transformation perspective de P en P' :
x' = dx / (y + d) et y' = (hy + dz) / (y + d)
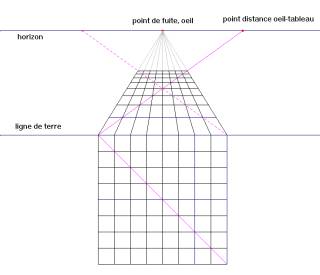
Une construction classique
Nous nous proposons d'abord de construire géométriquement l'image d'un point Q du plan du sol par la perspectivité que nous venons d'introduire.
Rabattons le plan du sol sur plan de la peinture, en utilisant la ligne de terre comme charnière, de manière à donner à l'axe Cy la direction opposée à celle de Cy'.
Notons T1 et T2 les points situés à la distance d du point T sur la parallèle à la ligne de terre menée par T. Le point T est évidemment l'image du point à l'infini commun aux perpendiculaires (dans le plan du sol) à la ligne de terre. Il est utile de remarquer que la perspectivité transforme la droite d'équation
x = y , z = 0 en la droite d'équation y' = hx' / d .
Les points T1 et T2 sont donc respectivement les images des points à l'infini des droites d'équations
x + y = 0 , z = 0 et x = y , z = 0 .
|
|
|
|
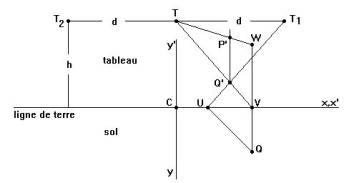
Du point Q menons le segment QV perpendiculaire à la ligne de terre et un segment QU qui fait un angle de 45 degrés avec cette même ligne. Le point intersection des droites VT et UT1 (ou UT2 suivant le choix de U) est le point image Q' cherché. Nous nous proposons maintenant de construire l'image d'un point P situé à la hauteur l sur la verticale (au plan du sol) passant par Q. Par V menons une perpendiculaire à la ligne de terre. Soit W le point d'ordonnée l (dans le plan du tableau) de cette perpendiculaire. L'intersection de la verticale passant par Q'et de la droite joignant W et T est le point P' recherché.
|
|
|
|
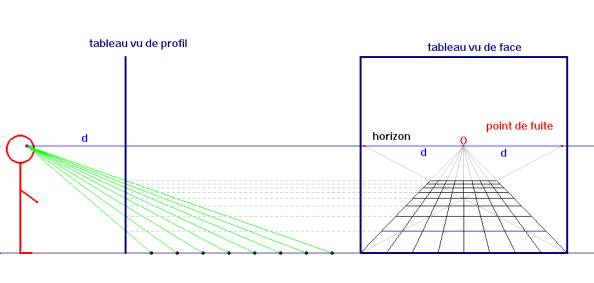
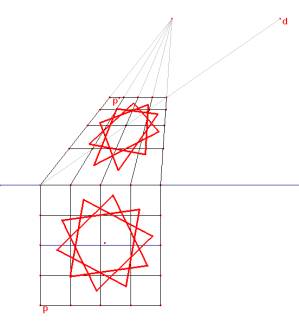
Voici la construction d’Alberti avec Cabri.
Nous avons créé une macro dont les paramètres sont le point G, la droite ligne de terre, le point O (point de fuite), le point D précisant la distance de l’oeil au tableau, le point P à représenter et la demi-droite rose (à 45°).
|
|
|
|
et quelques images de perspectives utilisant cette macro-construction.
|
|
|
Une anamorphose
|
|
|
|
|
|
Les anamorphoses les plus courantes sont des schémas marqués au sol des chaussées, dont le vélo étiré est un exemple classique. Une construction très simple permet d'obtenir la figure déformée. Imaginons que le dessin original soit tracé sur un plan p formant un angle u avec le sol. On projette alors le dessin sur le sol suivant la direction perpendiculaire au plan p. La transformation est décrite analytiquement par :
x ' = x y' = y / sin u
les axes x , x' sont situés sur la droite intersection des plans de la figure et du sol, les axes y , y' sont perpendiculaires à l'intersection.
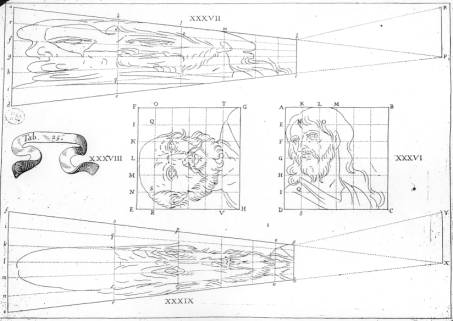
Anamorphose d’une chaise par Niceron
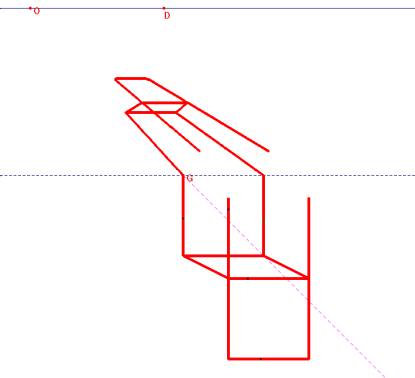
Imaginons qu'un artiste aît créé dans le plan du tableau la représentation perspective d'une scène. Quelque peu malicieux, notre artiste dépose la feuille de son dessin sur le plan du sol et refait une perspective de son premier dessin. Une question naturelle apparaît. Aurait-il pu gagner du temps et obtenir le résultat final en ne traçant qu'une seule perspective? Nous lui laissons toute liberté pour ce qui concerne la position du plan du tableau (qui pourra former un angle quelconque avec le sol). La réponse générale à la question est négative. La géométrie projective permet de justifier la réponse: le produit (de composition) de deux perspectivités n'est pas nécessairement une perspectivité.
Une voie royale de création d'anamorphoses est basée sur la propriété négative que nous venons de mettre en évidence.
Voici, avec un clin d'oeil à Niceron, une exemple concret. Nous avons tracé une chaise en perspective cavalière (une perspectivité dont le point d'oeil est situé à l'infini) et notre dessin est l'objet d'une perspective centrale. (Extrait du texte de Jean Drabbe)
|
|
|
|
Etude perspective d’une chaise Niceron La Perspective Curieuse 1638
|
|
|
|
|
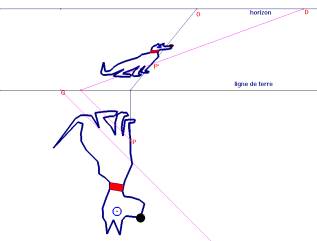
Planche de Niceron et anamorphoses d’un chien avec Cabri
|
|
4 Les peintres mathematiciens
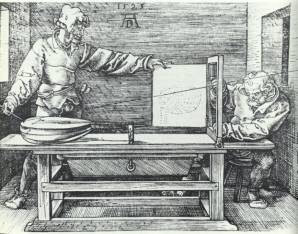
Albrecht Dürer (1471-1528)
Dürer introduit la méthode perspective en Europe du Nord après plusieurs voyages en Italie. Il écrit des livres comportant des constructions à l’intention des artistes. Ces instructions sont de véritables textes mathématiques.
Il écrit notamment en 1525 l’Underweysung dans lequel il utilise les doubles projections. Il construit des dispositifs permettant de matérialiser les effets de perspective dont le portillon de Dürer.
|
|
|
|
|
|
|
|
Le portillon de Dürer |
Le portillon construit par Lap Chung |
Léonard de Vinci (1452-1519)
Da Vinci, ingénieur, peintre, architecte, sculpter,incarne l’homme universel idéal de la Renaissance. Il écrit un traité sur la peinture.
|
|
|
|
Il semble que la première anamorphose connue serait la tête d’enfant dessinée par Leonard de Vinci en 1485 dans son Codex Atlanticus
Piero della Francesca (+/- 1410-1492)
Della Francesca écrit De prospectiva pingendi, un véritable manuel de mathématique à l’usage des peintres.
Sous le titre :
ET S'IL FAUT QUE TU METTES SUR UNE TABLE DE REPAS, OU DANS UN AUTRE PLAN RÉEL, UN RAFRAÎCHISSOIR AVEC SON PIÉDESTAL, LEQUEL PARAITRAÎT DRESSÉ AU-DESSUS DE LA DITE TABLE OU DANS LE DIT PLAN.
Piero della Francesca y décrit une anamorphose qu’il est très facile de réaliser. Il s'agit de représenter un verre dressé sur une table dont le dessin ne paraît correct que pour autant qu'il soit regardé à partir d'une position convenable au-dessus de la feuille. Le problème, formulé dans le cadre de la géométrie descriptive, reçoit une solution aisée. Nous imaginons que le plan de la table soit le plan horizontal de projection et qu'un plan (vertical) de symétrie du verre soit choisi comme plan vertical de projection. Nous supposons que l'oeil soit placé dans ce plan vertical. Il nous faut construire la projection centrale du verre, à partir de l'oeil, sur le plan horizontal de projection. Il suffit de déterminer les images des points situés dans le plan vertical de projection et de réaliser que les images des sections du verre par des plans horizontaux sont des cercles. Dans la figure présentée ci-après, nous avons effectué une rotation d'un quart de tour afin de faire apparaître verticalement le verre de Piero della Francesca (Extrait du texte de Jean Drabbe).
|
|
|
|
La construction réalisée avec Cabri et celle de Piero.
|
|
|
|
Hans Holbein le Jeune (1497-1543)
Au XVIe siècle, dans les premières anamorphoses, l’image est allongée géométriquement pour perdre son aspect figuratif. Le spectateur ne découvre le sujet que dans une vision oblique rasant le tableau.
En ‘Les ambassadeurs’, le peintre représente deux jeunes ambassadeurs français à la cour du roi d’Angleterre. Ils s’appuient sur une table recouverte d’un tapis et d’objets symboliques: des appareils pour observer le monde, des livres et des instruments de musique. Cette vanité expose les outils de la science et les attributs du monde terrestre éphémère.
|
|
|
|
|||||
|
|
Hans Holbein: Les ambassadeurs |
|
Une forme ovoïde apparaît au bas du tableau : Le spectateur reconnaît l’image d’un crâne en regardant le tableau en vision oblique. Ce crâne serait la représentation métaphorique du triomphe de la mort sur les hommes de culture, de pouvoir et de science. Ci-contre, nous avons photographié la « chose » sur une reproduction du tableau. D’abord de face, puis à partir du bord droit du tableau à mi-hauteur sous des angles d’incidence de plus en plus réduits jusqu’à toucher le plan du tableau. La « chose » se transforme progressivement en l’image d’un crâne humain et les proportions de ce crâne ne deviennent réalistes que sous un angle de vue rasant la surface du tableau. |
|
|
|
|
|
|
|
|
|
|
|
|
5 L ’anamorphose conique
(Extraits du texte de Jean Drabbe)
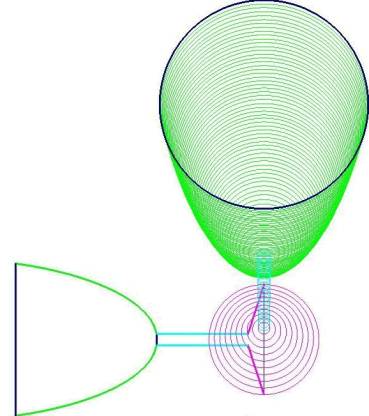
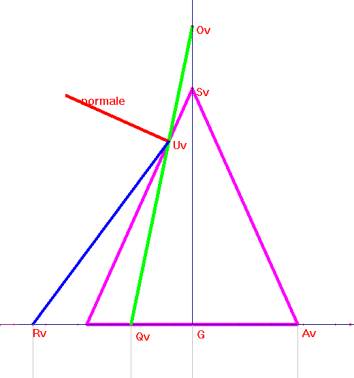
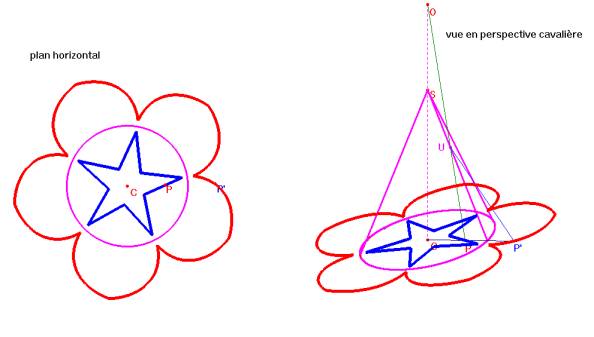
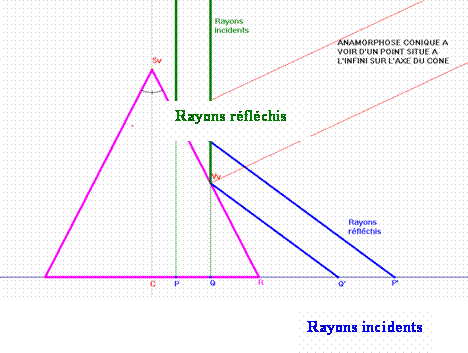
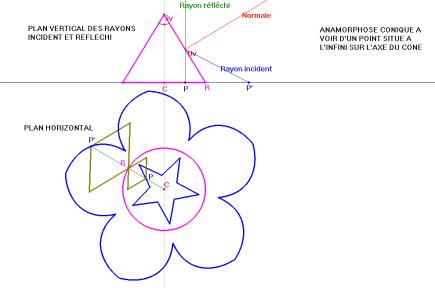
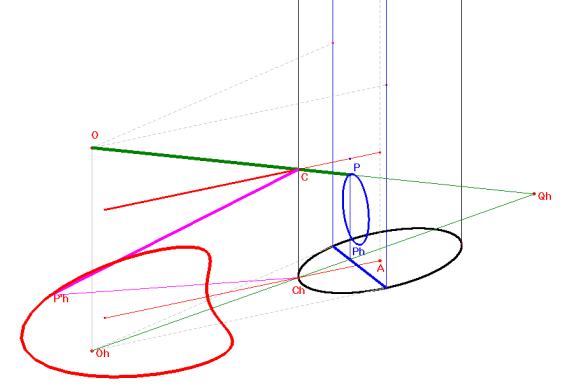
Supposons qu'un cône (de révolution) réfléchissant soit posé sur une table sur laquelle une figure F a été tracée. L'oeil O placé sur l'axe de révolution, au-dessus du sommet S, perçoit, après réflexion sur la surface latérale, une image F' qui lui paraît provenir également de la surface de la table.
Le problème qui nous intéresse est de déterminer F de manière telle que F' soit une figure préalablement imposée. Une solution analytique est donnée dans l'article de Hunt mentionné dans la bibliographie. Nous allons traiter la question de manière graphique en utilisant des méthodes élémentaires de la géométrie descriptive.
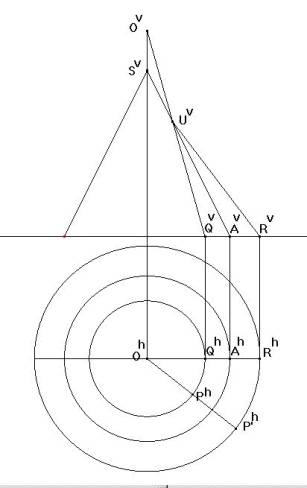
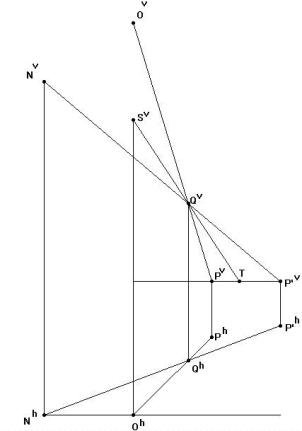
|
Le plan horizontal (de projection) sera le plan de la table et le plan vertical de projection sera un plan vertical passant par l'axe du cône. Soit P un point de la table. Nous souhaitons trouver un point P' de la table tel qu'un rayon lumineux issu de P' soit réfléchi suivant la droite PO. Les lois de la réflexion fournissent une solution immédiate pour les points P situés dans le plan vertical (de projection). Nous allons donc ramener le cas général à ce cas particulier. Imposons à l'espace une rotation autour de l'axe de symétrie du cône qui amène le point P sur un point Q situé dans le plan vertical. Le rayon réfléchi UO (qui prolonge QU) provient d'un rayon incident RU émanant d'un point R de la table. La rotation inverse de celle utilisée précédemment amène R en le point P' recherché. |
|
Voici la figure que nous avons créée avec Cabri. Elle montre les projections verticales et horizontales du cône avec la construction des points P et P’. |
|
|
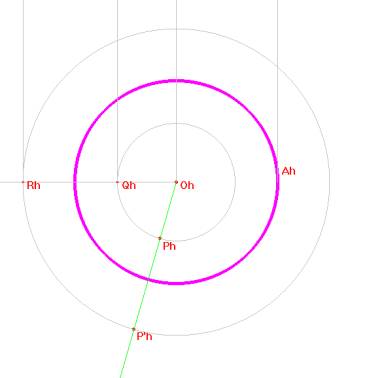
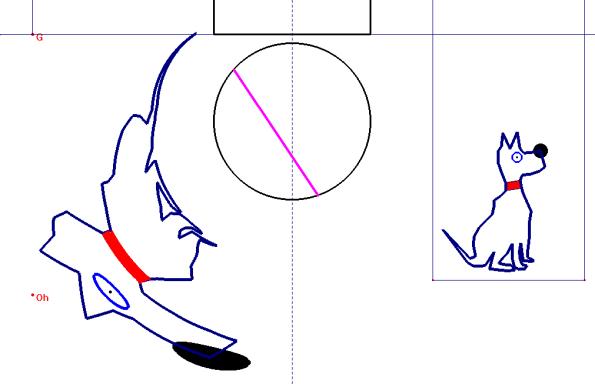
Pour réaliser les images qui vont suivre, nous avons crée une macro-construction dont les paramètres sont le point G, la droite (ligne de terre) les points Ov projection verticale de l’oeil, Sv projection verticale du sommet du cône, Oh projection horizontale de l’oeil, Ah projection horizontale du point permettant de modifier la base du cône et Ph le point à anamorphoser dans le plan horizontal. |
|
|
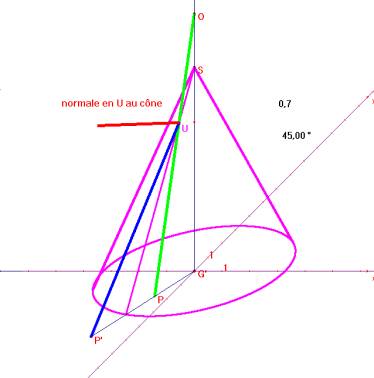
L’autre partie de la figure Cabri montre en perspective cavalière le cône de la page précédente. |
|
|
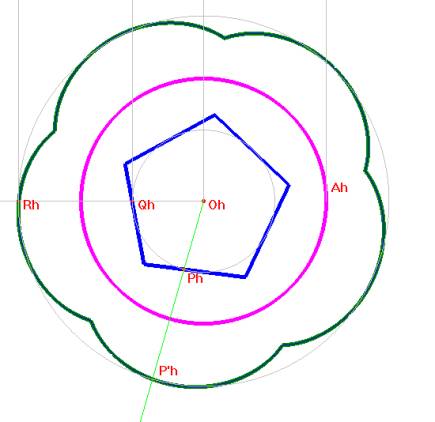
Voici une anamorphose que nous avons réalisé avec Cabri à voir d’un point situé à une distance finie du sommet du cône. Les couleurs remplissant le dessin ont été ajoutées en utilisant le logiciel Paint Shop Pro. |
|
Image anamorphosée d’un pentagone
|
Vue en perspective |
|
|
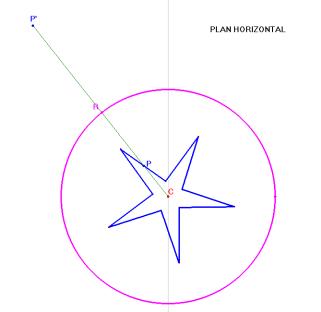
Vue dans le plan horizontal de projection |
|
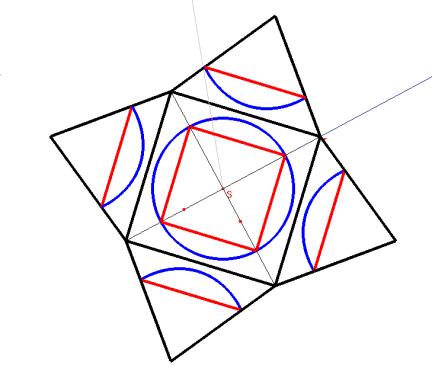
Anamorphose conique d’une étoile
|
|
|
|
|
|
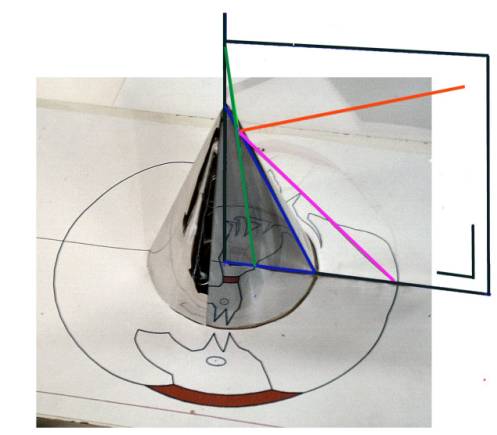
Modèle formé d’un cône en partie transparent et en partie réfléchissant montrant l’anamorphose d’un chien et la construction pour un point de ce dessin.
|
|
|
|
|
|
|
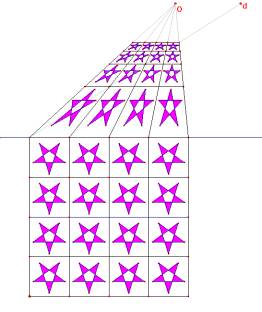
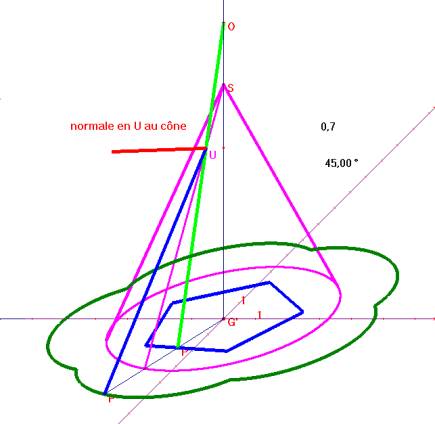
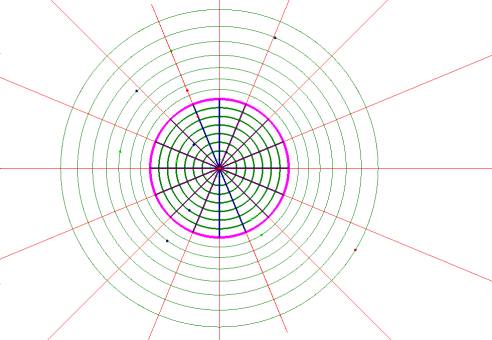
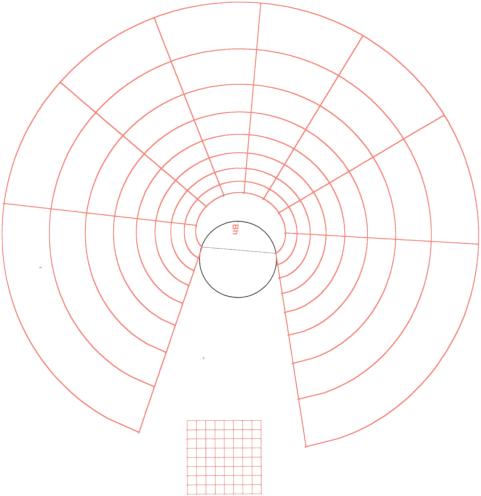
En utilisant la macro on peut créer l’image d’une grille de correspondance qui permet de faire des dessins anamorphosés.
Cas particulier des anamorphoses coniques: L’oeil de l’observateur se trouve a l’infini sur l’axe du cone
Les rayons venant de O sont parallèles á l’axe du cone.
|
|
|
|
|
Par les propriétés des triangles semblables, le rapport PR / P’R est constant quelque soit P. |
|
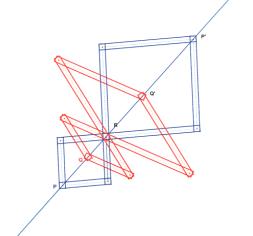
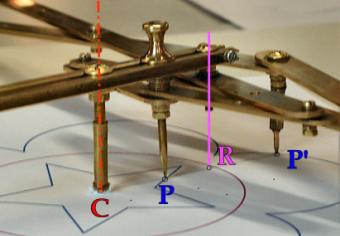
Le pantographe de Steiner-Parre (oeil à l’infini)
|
|
Le pantographe de SCHEINER (1605) permet de tracer mécaniquement des homothéties. Il a été utilisé par Michel PARRE (1973) pour réaliser un appareil permettant de tracer mécaniquement les anamorphoses coniques observées de l’infini. Nous avons fait réaliser par Jean-Jacques Gabriel cet instrument d’après un modèle conçu avec Cabri. |
|
L’ensemble consiste en un pantographe simple tournant autour du centre de la base du cône et qui centré sur le cercle, maintient un rapport constant entre la distance au cercle du point que l’on voudra voir et la distance au cercle du point à dessiner sur l’anamorphose. |
|
|
|
|
|
Figure cabri qui en s’animant montre la réalisation d’une anamorphose et le mouvement du pantographe.
Le pantographe et une réalisation d’anamorphose et son image sur le cône
|
|
|
|
|
Anamorphose conique d’un chien réalisée avec Cabri (à voir de l’infini)
|
|
|
|
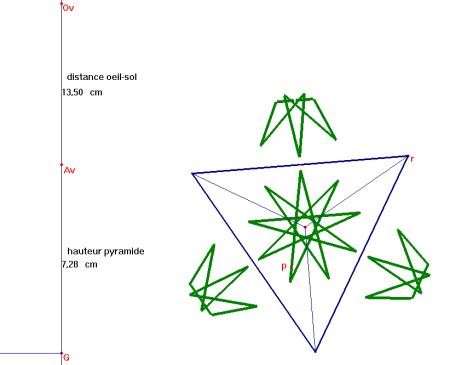
6 L’anamorphose pyramidale
(Extrait du texte de Jean Drabbe)
Bien qu'elles soient rarement utilisées par les artistes, les anamorphoses pyramidales ne posent aucune difficulté géométrique mais demandent quelques utilisations astucieuses à Cabri.
|
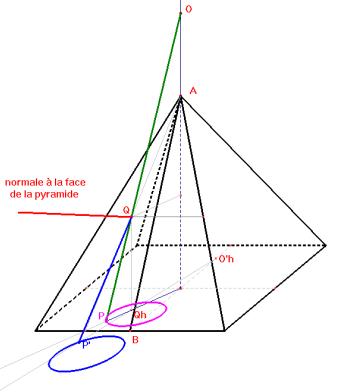
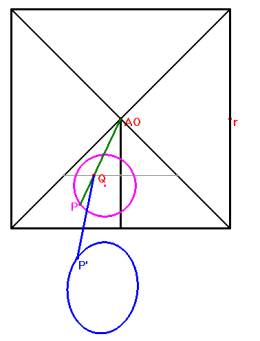
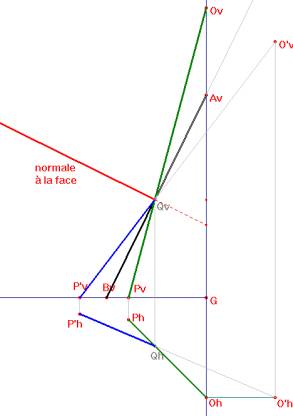
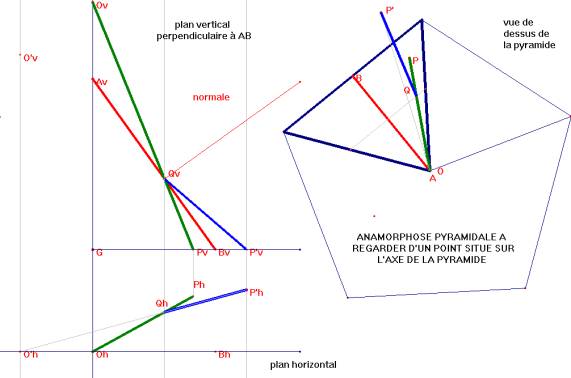
Nous supposons qu'une pyramide réfléchissante soit posée sur le plan horizontal de projection. L'oeil O est placé sur la verticale passant par le sommet A de la pyramide. Les objets situés dans plan horizontal qui se réfléchissent sur la pyramide semblent apparître dans la base de celle-ci. Soit P un point de la base de la pyramide. Nous devons déterminer le point P' du plan horizontal tel qu'un rayon issu de P' se réfléchisse suivant PO. Il suffit évidemment de traiter le problème pour une face f de la pyramide, face que nous supposerons (sans perte de généralité) perpendiculaire au plan vertical de projection, coupant celui-ci suivant AB. Notons Q le point de percée de OP dans f et O’ le symétrique de O par rapport à f. Une propriété élémentaire des miroirs plans montre que la droite P'Q doit passer par O’.Le problème est ainsi résolu. |
|
Figure Cabri montrant une pyramide à base carrée en perspective cavalière et l’image anamorphosée d’un cercle réfléchie sur la face frontale. |
|
|
La base carrée de la pyramide et les projections verticales et horizontales de cette pyramide avec la construction des points P et P’.
|
|
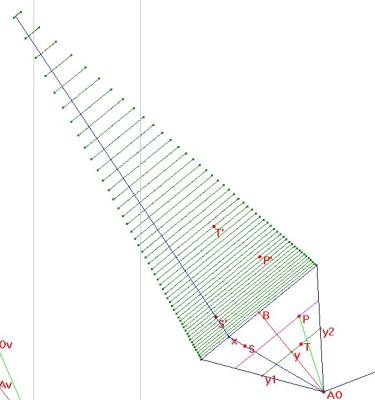
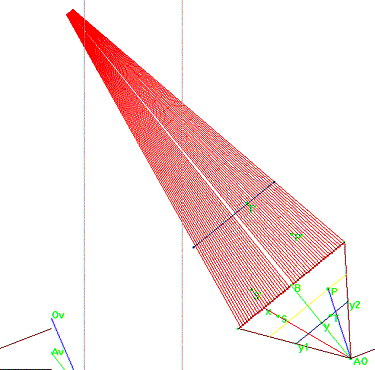
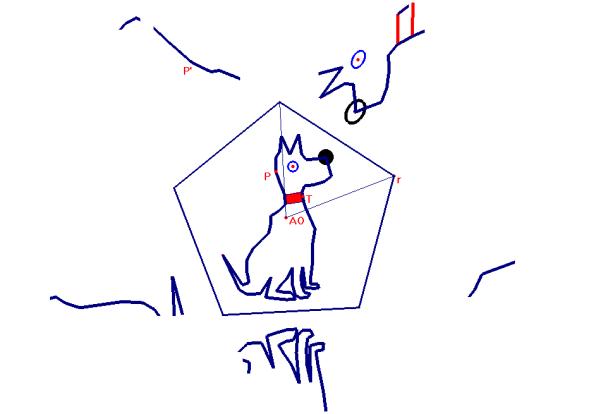
Pyramide à base pentagonale avec un point P et son image anamorphosée P’
|
|
|
|
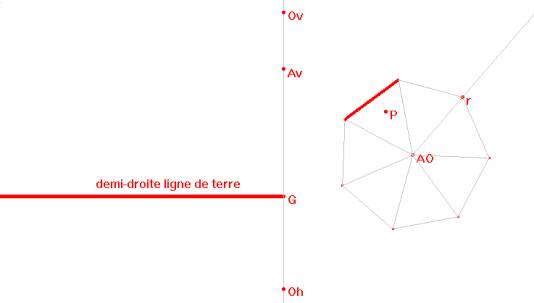
Nous avons crée une macro-construction dont les paramètres sont le point G, la demi-droite horizontale comprenant G (ligne de terre), la projection verticale Av du sommet de la pyramide, la projection verticale Ov de l’oeil situé sur l’axe de la pyramide, sa projection horizontale Oh
le point AO centre du polygone de base et le point r déterminant la grandeur de la base,
le point P à voir et le segment déterminant la face de la pyramide sur laquelle on travaille.
|
|
|
|
|
Le modèle en 3 dimensions utilisé pour expliquer notre construction. |
|
|
|
|
|
|
|
|
Voici la trace des images des segments verts y1 y2 lorsque y varie sur AO B et la trace rouge des segments x AO lorsque x varie sur le coté de la face.
|
|
|
|
Pyramide à base carrée et images anamorphosées d’un cercle et d’un carré
|
|
|
|
Le dessin et la réflexion sur la pyramide
|
|
|
|
|
|
|
|
Images cabri d’un chien anamorphosé sur une pyramide à base pentagonale et d’un polygone étoilé sur une pyramide à base triangulaire.
|
|
|
|
7 L ’anamorphose cylindrique
(Extraits du texte de Jean Drabbe)
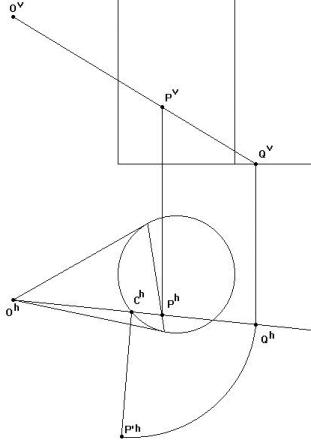
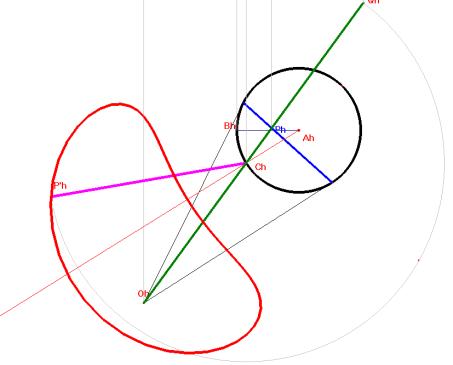
Supposons qu'un cylindre (de révolution) réfléchissant soit posé sur le plan horizontal de projection et que l'oeil soit placé en O. Les images situées dans le plan horizontal semblent se réfléchir dans le plan de contact déterminé par les plans tangents issus de O. Soit un point P dans ce plan de contact. Nous devons déterminer un point P' du plan horizontal tel qu'un rayon lumineux issu de P' soit réfléchi suivant la droite PO. La solution fournie par Kirsti Andersen (voir son article repris dans la bibliographie) s'inscrit naturellement dans le cadre d'un traitement par la géométrie descriptive.
|
Soit Q le point de percée de OP dans le plan horizontal de projection. La droite OP rencontre la surface cylindrique en deux points. Notons C celui situé entre O et P. Les distances ChP'h et ChQh devant être égales, le point P' est complètement déterminé par le fait que OhCh et P'hCh forment des angles égaux avec la tangente en Ch au cercle de base. |
|
Construction de base vue en perspective cavalière.
|
|
|
|
|
|
|
Construction de l’image d’un cercle par anamorphose cylindrique en utilisant la géométrie descriptive et Cabri.
|
|
|
|
|
|
|
|
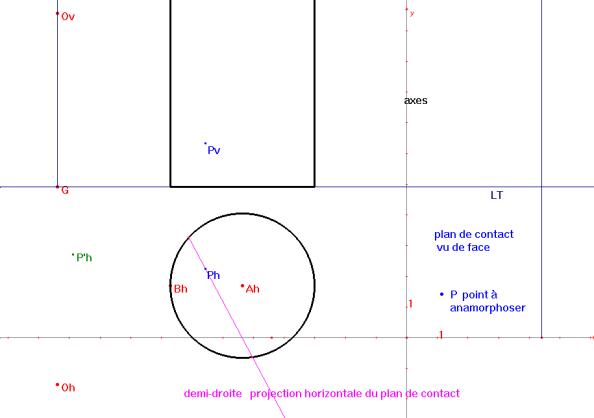
Pour réaliser les images qui vont suivre, nous avons crée une macro-construction dont les paramètres sont le point G, la droite (ligne de terre) les points Ov projection verticale de l’oeil, Oh projection horizontale de l’oeil, Ah centre de la base du cylindre, Bh point déterminant le rayon de cette base, les axes du plan de contact vus de face, P le point à anamorphoser dans le plan de contact vu de face et la demi-droite projection horizontale du plan de contact.
|
|
|
|
|
|
|
|
|
|
|
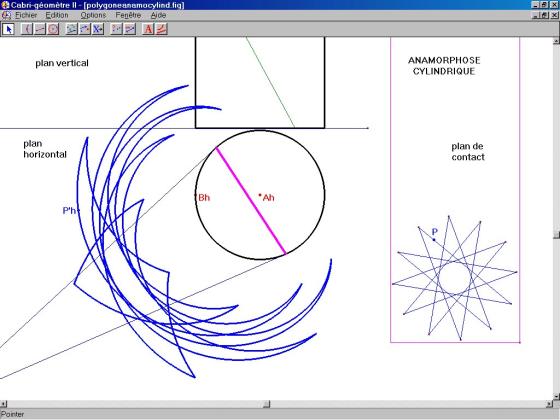
Voici créée à l’aide de notre macro l’image d’une grille de correspondance pour l’ anamorphose cylindrique
|
|
|
|
Anamorphose cylindrique: Niceron déforme en anamorphose cylindrique le portrait de Saint-François de Paule réalisé par Simon Vouet. (J-F Nicéron 1638)
|
|
|
|
L’anamorphose cylindrique d’un chien réalisée avec notre macro-construction.
|
|
|
|
Bibliographie de la partie mathematique
Ades, D. (editor) Dali's Optical Illusions, Wadsworth Atheneum Museum of Art in association with Yale University Press, 2000.
Alberti, L. On painting (translated with introduction and notes by J.R. Spencer), Yale University Press, 1956.
Andersen, K. The mathematical treatment of anamorphoses from Piero della Francesca to Niceron in History of Mathematics: States of the Art, Academic Press, 1996.
Baltrusaitis, J. Anamorphoses ou magie artificielle des effets merveilleux , Olivier Perrin (France), 1969.
Collins, D. Anamorphosis and the Eccentric Observer, parts 1 and 2, Leonardo 25 (1992), No. 1 and 2.
Dürer, A. Géométrie (présentation et traduction de Jeanne Peiffer), Seuil (Paris), 1995.
Euclide L'optique et la Catoptrique, oeuvres traduites pour la première fois en français par Paul Ver Eecke, Librairie scientifique et technique Albert Blanchard (Paris), 1959.
L'ouvrage contient La recension de l'optique d'Euclide par Héron d'Alexandrie.
Flocon, A. et Taton, R. La perspective, PUF (1963).
Frangenberg, T. The angle of vision : problems of perpectival representation in the fifteenth and sixteenth centuries, Renaissance Studies, 6 (1992), pp. 1-45.
Füsslin, G. und Hentze, E. Anamorphosen, Füsslin Verlag (Stuttgart), 1999.
Godeaux, L. Géométrie projective, Sciences et Lettres, Liège (1952).
Hunt, J. et al. Anamorphic images, American Journal of Physics, 68 (2000), pp. 232-237.
Monge, G. Géométrie Descriptive, augmentée d'une théorie des ombres et de la perspective extraite des papiers de l'auteur par B. Brisson, Gauthier-Villars, Paris (1922).
Niceron, J. La perspective curieuse (1652). Microfilm m9159 de le Bibliothèque Nationale de France.
Ozanam, J. Récréations mathématiques et physiques, qui contiennent les problèmes & les questions les plus remarquables, & les plus propres à piquer la curiosité, tant des mathématiques que de la physique... . Tome second. Contenant la mécanique & l'optique, avec l'acoustique & la musique / par feu M. Ozanam,... ; nouv. éd., totalement refondue & considérablement augm. par M. de C.G.F. [Chanla, géomètre forézien], édition C.A. Jombert (Paris), 1778. Le texte est disponible sur le site gallica.bnf.fr de la Bibliothèque Nationale de France.
Piero della Francesca De la perspective en peinture (traduit et annoté par J-P. Le Goff). In Media Res (Paris), 1998.