Die Methodologie klassischer Testverfahren und die der explorativen Datenanalyse sind grundsätzlich verschieden. Werden im Unterricht Testverfahren zur Datenanalyse eingesetzt, wie dies häufig geschieht, können Schüler die Grundlagen der Testverfahren nicht verstehen, sondern nur lernen, Rezepte schematisch anzuwenden. An zwei Beispielen wird der Unterschied, zwischen statistischer und inhaltlicher Absicherung von Hypothesen aufgezeigt.

 

1. Vorbemerkungen

Viele Mathematiklehrpläne der Sekundarstufe II enthalten den Hinweis, dass an geeigneten Stellen erkenntnistheoretische Fragestellungen behandelt werden sollten. Die Realisierung in der Schulpraxis setzt aber voraus, dass die Schüler auftretenden Probleme als relevant erkennen und selbständig Lösungen finden können. Eine solche Stelle liegt im Stochastikunterricht beispielsweise beim retrospektiven Einsatz klassischer Testverfahren vor, bei dem schon vorliegende Daten nachträglich einem Test unterworfen werden.

 

2. Wie statistische Aussagen zustande kommen – Die übliche Vorgangsweise

In vielen Schulbüchern findet man mit geringen Abwandlungen das folgende Beispiel.

Beispiel 1 – Lottozahlen:

Die nachfolgende Übersicht zeigt die Ziehungshäufigkeit der Lottozahlen nach 996 Ziehungen (November 1974):

 

Dieser Datensatz zeigt, dass 13 die Zahl  mit der kleinsten Ziehungshäufigkeit war. Kann man aufgrund der vorliegenden Ziehungshäufigkeit mit einer statistischen Sicherheit von 95% ausschließen, dass 13 eine Unglückszahl ist?

Bei der Lösung wird in den Schulbüchern im allgemeinen etwa folgendermaßen argumentiert: Wir gehen davon aus, dass die Lottoziehung nicht manipuliert war, und wählen daher als Nullhypothese ‚Die Wahrscheinlichkeit p für das Auftreten von 13 bei einer Ziehung ist 6/49’ Da 13 die kleinste Ziehungshäufigkeit hat, ist es naheliegend, als Gegenhypothese ‚p < 6/49’ zu wählen, also einseitig zu testen.

 

Fig. 1

 

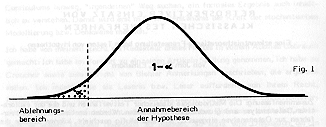
Die weitere Lösung wird dann etwa so durchgeführt: Bei 996 Ziehungen wird man jede der Zahlen von 1 bis 49 etwa

also ca. 122-mal erwarten. Die Standardabweichung beträgt

Beim einseitigen Test mit  a = 5%  wird die Grenze des Ablehnungsbereichs bestimmt durch

Mit den oben bestimmten Werten ergibt sich somit für die Grenze des Ablehungsbereichs

Das bedeutet: Der Ablehnungsbereich reicht von 0 bis 104. Die von 13 erreichte Häufigkeit, nämlich 96, liegt daher im Ablehnungsbereich. Also, so wird dann argumentiert, kann man mit 95% Sicherheit nicht ausschließen, dass 13 eine Unglückszahl ist.

Anmerkung: Bei einem Signifikanzniveau von 5% würde man auch mittels eines zweiseitigen Tests, d.h. bei der Gegenhypothese ‚’p¹6/49’, zu demselben Schluss kommen, denn der Ablehnungsbereich würde dann linksseitig bis 101 reichen.

Die Lotto-Aufgabe zeigt exemplarisch, auf welche Art viele statistische Testaussagen zustande kommen: Ausgangsbasis ist ein vorhandener Datensatz (hier: Häufigkeit der Lottozahlen). Dieser Datensatz zeigt gewisse Auffälligkeiten (hier: geringe Ziehungshäufigkeit der Zahl 13). Man setzt einen Test an, um diese Auffälligkeiten an demselben Datensatz auf Signifikanz zu prüfen. So zeigt auch die folgende Anwendung diese Struktur:

Beispiel 2 – Maschinenstillstände:

In einem Werk werden einen Monat lang die Maschinenstillstände einer Schicht notiert, um zu prüfen, ob die Wahrscheinlichkeit hierfür in gewissen Stunden der Schicht besonders groß ist.

 

Weicht die Anzahl der Maschinenstillstände in der ersten Stunde (Auffälligkeit: größte Häufigkeit) signifikant von der mittleren Anzahl der Maschinenstillstände ab?

Ähnlich arbeitet man in vielen Bereichen, in denen die Statistik eingesetzt wird: Ein Datensatz mit gewissen Auffälligkeiten liegt vor, beispielsweise erhöhte Krebserkrankungen in gewissen Gebieten, erhöhtes Waldsterben in gewissen Regionen, verringerte Unfallzahlen zu gewissen Zeiten, Einfluss von Chemikalien auf gewisse Umweltfaktoren, Arzneimittelwirkung auf gewisse Organe, Ergebnisse von psychologischen Tests in gewissen Gruppen usw. Diese Auffälligkeiten prüft man dann mit demselben Datenmaterial in einem Testverfahren auf statistische Signifikanz.

 

3. Ist die übliche Vorgangsweise einwandfrei? — Gewinnung versus Testen von Hypothesen

Ist die übliche Vorgangsweise einwandfrei? Um eine Antwort auf diese Frage zu erhalten, betrachten wir wieder das obige Lottozahlen-Beispiel.

 

Beispiel 3 – Lottozahlen (Fortsetzung):

Auch wenn alle Zahlen die gleiche Ziehungswahrscheinlichkeit haben, wird man nicht erwarten, dass alle mit der gleichen Häufigkeit gezogen werden. Eine der gezogenen Zahlen wird die geringste Ziehungshäufigkeit haben. Bis zur 996-ten Ziehung beim Samstag-Lotto war dies die Zahl 13. Die zu testende Vermutung ‚13 ist eine Unglückszahl’ ist nicht unabhängig von den Daten entstanden, die zum Test herangezogen werden, sondern aus diesen gewonnen worden. Entscheidend ist: Der Test wurde also nicht mit irgendeiner der Zahlen von 1 bis 49 durchgeführt, sondern mit der Zahl, von der man weiß, dass sie die geringste Ziehungshäufigkeit hatte.

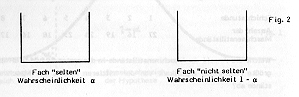
Wir bestimmen näherungsweise die Wahrscheinlichkeit dafür, dass mindestens eine Zahl mit ihrer Ziehungshäufigkeit im Ablehnungsbereich der Hypothese liegt, also ‚selten’ ist. Eine einfache Modellvorstellung hilft: Kugeln mit den Zahlen von 1 bis 49 werden auf zwei Fächer ‚selten’ und ‚nicht selten’ mit den Wahrscheinlichkeiten a bzw. 1-a verteilt:

 

Fig. 2

 

 

Die Wahrscheinlichkeit, dass alle 49 Kugeln ‚nicht selten’ sind, beträgt demnach

Für die Wahrscheinlichkeit W, dass mindestens eine Kugel ‚selten’ ist, ergibt sich:

Für  a=5%  folgt somit  W=0,919. Das bedeutet: Die Wahrscheinlichkeit, dass mindestens eine Zahl ‚selten’ ist, beträgt bei dieser Wahl von  a  ungefähr 92%. Wenn aber eine Zahl ‚selten’ ist, dann ist es mit Sicherheit insbesondere auch die mit der kleinsten Ziehungshäufigkeit. Also:

Das Ergebnis, dass die Zahl der kleinsten Ziehungshäufigkeit (in dem Lottozahlen-Beispiel die Zahl 13) ‚’selten’ ist, also in den Ablehnungsbereich des Tests mit dem Signifikanzniveau  a=5%  fällt, ist überhaupt nicht verwunderlich, sondern mit großer Wahrscheinlichkeit, nämlich mit 92%, zu erwarten.

Anmerkung: Die Wahrscheinlichkeit dafür, Kugeln im Ablehnungsbereich zu finden, kann gut durch Simulation bestimmt werden. Oft finden Schüler gerade dadurch ein ‚Gefühl’ für das Problem. Der zugehörige Algorithmus ist einfach; er zeigt darüber hinaus den Hintergrund der o.a. Näherung auf: Die Schritte sind nicht unabhängig voneinander. Wenn nämlich eine Zahl ‚selten’ ist, müssen andere entsprechend häufiger auftreten.

Die Behandlung des Beispiels zeigt: Ein einzelner gegebener Datensatz kann entweder zur Gewinnung oder zum Testen von Hypothesen dienen.

 

4. Verbesserte Vorgangsweise beim Testen — statistische und inhaltliche Prüfung von Hypothesen

Wenn ein Datensatz für das Aufstellen einer Hypothese benutzt wird, dann muss die Hypothese entweder statistisch durch einen anderen davon unabhängigen Datensatz oder inhaltlich überprüft werden. Wir betrachten zunächst die Möglichkeit der statistischen Überprüfung. Dazu wählen wir wieder das Lottozahlen-Beispiel.

Beispiel 4 – Lottozahlen (Fortsetzung):

Im November 1974 nach 996 Ziehungen war 13 die Zahl mit der geringsten Ziehungshäufigkeit (96-mal). Die Abweichung vom erwarteten Mittelwert  m=n*p»122  war signifikant. Zu diesem Zeitpunkt hätte man die Hypothese ‚13 ist eine Unglückszahl’ aufstellen können, d.h. die Ziehungshäufigkeit von 13 ist signifikant kleiner als die der anderen Lottozahlen.

Dann hätte man beispielsweise die nächsten 520 Ziehungen bis zum 17. Oktober 1984 abwarten können. Das neugewonnene (vom vorigen Datensatz unabhängige) Datenmaterial zeigt dann: In den 520 Ziehungen ist die Zahl 13 insgesamt 54-mal gezogen worden. Die Abweichung vom erwarteten Mittelwert

ist nicht signifikant: Wegen

liegt die Ziehungshäufigkeit der Zahl 13 im Annahmebereich der Hypothese, denn die Grenze zwischen Annahme- und Ablehnungsbereich liegt zwischen 51 und 52. Die an dem im November 1974 vorliegenden Datenmaterial aufgestellte Hypothese ‚13 ist eine Unglückszahl’ wird also durch das neue, unabhängig gewonnene Datenmaterial nicht gestützt.

Anmerkungen:

1) Betrachtet man alle 1516 Ziehungen des Samstag-Lotto 6 aus 49 (Stand 27. Oktober 1984), so ist die Zahl 13 genau 150-mal gezogen worden. Die Abweichung vom Mittelwert ist signifikant. Dieser Datensatz ist aber nicht unabhängig vom ersten (996 Ziehungen), sondern enthält diesen als Untermenge.

2) Man könnte im Prinzip auch eine inhaltliche Überprüfung der Hypothese vornehmen, z.B. nachprüfen, ob der Zufallsmechanismus beim Lotto nicht einwandfrei war, oder, ob sich die Beschaffenheit der Kugel 13 von der der anderen Kugeln unterscheidet. Natürlich wird man das in diesem Fall mit ziemlicher Sicherheit ausschließen können.

Die an einem Datensatz gewonnene Hypothese kann auch inhaltlich gestützt oder widerlegt werden. Betrachten wir dazu das Beispiel mit den Maschinenstillständen.

Beispiel 5 – Maschinenstillstände (Fortsetzung):

Das vorliegende Datenmaterial zeigt, dass die Anzahl der Maschinenstillstände in der ersten Stunde am größten ist. Die Firma kann nun beispielsweise einen Arbeitswissenschaftler beauftragen, zu untersuchen, ob dieser Befund eine Erklärung hat, z.B., ob die Maschinen in einem schlechten Zustand auf die nächste Schicht übergeben werden. Die Arbeiter der nächsten Schicht müssten dann in der ersten Stunde die Maschinen relativ oft stilllegen, um diese zu warten. Es könnte sein, dass die Maschinenstillstände in der ersten Stunde arbeitspsychologisch zu erklären sind, z.B. durch Anlaufschwierigkeiten o.ä.

Anmerkung: Auch im Beispiel mit den Maschinenstillständen könnte man die Vermutung durch einen zweiten, unabhängigen Datensatz statistisch zu stützen oder zu widerlegen versuchen. In erster Linie wird diese statistische Prüfung an einem weiteren Datensatz dadurch nahegelegt, dass eine tragfähige inhaltliche Erklärung und Absicherung der aufgestellten Hypothese nicht gefunden werden konnte.

Verwendet man weder die Information über schlechte Schichtstunden aus denselben Daten noch andere Informationen beispielsweise aus früheren Daten, so kann man nur einen undifferenzierten, auf keine spezifische Hypothese eingehenden Chi-Quadrat-Test auf Gleichverteilung (Chi-Quadrat=6, df=7) ansetzen. Sein Ausfall zeigt, dass das vorliegende empirische Ergebnis sich nicht als signifikant im statistischen Sinne einstufen lässt, d.h. dass die Schwankungen der beobachteten Daten noch als zufällig angesehen werden müssen.

Die mit dem Chi-Quadrat-Test verbundene Annahme (‚fehlendes inhaltliches Wissen’) und die aus dem Ausfall des Chi-Quadrat-Tests resultierende Einsicht (‚keine Signifikanz’) legen nahe, einen neuen Datensatz für eine statistische Prüfung zu erheben. Lässt man umgekehrt die dem Chi-Quadrat-Test zugrundeliegende Annahme (‚kein inhaltliches Wissen zur Absicherung der spezifischen Hypothese’) fallen, so liegt es gerade dadurch nahe, sich zunächst fehlendes Wissen zu beschaffen, beispielsweise durch neues Datenmaterial. Neben einer weiteren statistischen Untersuchung ist es sinnvoll, alle Anstrengungen auf eine bessere inhaltliche Durchdringung der anstehenden Frage zu lenken!

Eine Analyse der Bedeutung statistischer Aussagen, insbesondere im Zusammenhang mit dem Chi-Quadrat-Test, findet man in Borovcnik (1984).

Am Beispiel mit den Maschinenstillständen kann man leicht klar machen: Auffälligkeiten im Datenmaterial können inhaltlich erklärt werden, wenn man die Einflussfaktoren kennt. Dies gilt z.B. auch für die Ursachen von Krebserkrankungen, Waldsterben sowie Verkehrsunfällen. Auffälligkeiten in einem Datensatz können etwa die Richtung einer wissenschaftlichen Untersuchung bestimmen.

Anmerkung: Auffälligkeiten im Datenmaterial aufzuspüren und zu untersuchen wird bisher in der Schule zu wenig behandelt. Retrospektives Testen kann als Hilfsmittel der sogenannten Explorativen Datenanalyse eingesetzt werden. In dieser Verwendung ist retrospektives Testen durchaus sinnvoll (siehe etwa P. Ihm 1980). Darüber hinaus bietet die Explorative Datenanalyse anschauliche graphische Methoden: Diese bieten eine große Chance für den Stochastikunterricht.

 

5. Die Problematik von ‚vorher’ und ‚nachher’

Eine immer wieder beklagte methodische Schwierigkeit beim Unterrichten von Testverfahren in der Schule beruht gerade darauf, dass zwischen ‚vorher’ und ‚’nachher’ nicht sorgfältig unterschieden wird. Dies soll an einem weiteren bekannten Beispiel erläutert werden.

 

Beispiel 6 – Arzneimittel:

Ein Hersteller behauptet, dass ein Medikament in 70% der Fälle bei einer bestimmten Krankheit hilft. Ein Test im Krankenhaus ergab, dass 15 von 25 Patienten gesund wurden. Kann die Hypothese ‚Heilungschance beträgt 70%’ aufrechterhalten werden?

Bei dieser Aufgabe, so wird bemerkt, bestimmen die Schüler die Bernoulli-Wahrscheinlichkeiten B(25;0,7; X=15) und argumentieren, dass dieses Ergebnis sehr selten sei; es sei nicht leicht, die Schüler dazu zu bringen, die kumulierten Wahrscheinlichkeiten B(25;0,7; X£15) zu betrachten. Diese Schwierigkeit sollte m.E. nicht durch automatisierte Verfahren übergangen werden, sondern sollte vielmehr durch geeignete Aufgabenstellung und Analyse behoben werden.

 

Beispiel 7 – Arzneimittel (Fortsetzung):

Ein Hersteller vermutet aufgrund seiner Laboruntersuchungen, dass ein Medikament in 70% der Fälle bei einer bestimmten Krankheit hilft.

a) Welches Testverfahren einseitig/zweiseitig und welches Signifikanzniveau ist angemessen?

b) Entscheide, ob die Hypothese ‚Heilungschance beträgt 70%’ abgelehnt werden muss, wenn eine Testdurchführung in einem Krankenhaus ergab, dass 15 von 25 Patienten gesund wurden.

Der Verwerfungsbereich wird bestimmt, bevor das Ergebnis der Testdurchführung vorliegt.

Anmerkung: Es ist ein elegantes und in der Praxis häufig verwendetes Verfahren, das nominelle Signifikanzniveau, den sogenannten p-Wert, zu ermitteln, das durch ein schon vorliegendes Testergebnis bestimmt wird. Man nimmt dieses Ergebnis als Grenze zwischen Verwerfungs- und Annahmebereich und bestimmt die Summe der Wahrscheinlichkeiten für dieses und alle ‚extremeren’ Ergebnisse. Die Formulierung deutet schon an, dass man sich vorstellt, das Ergebnis sei noch nicht eingetreten.

 

6. Abschließende Bemerkungen

Die angesprochene Problematik beim Testen von Hypothesen ist Schülern nicht ohne weiteres einsichtig. Zu Beginn der Problemstellung wird im Klassengespräch etwa geäußert: ‚Entweder ist die Abweichung gewisser Merkmalsausprägungen signifikant oder nicht. Darum spielt es keine Rolle, ob Hypothese und Test vor oder nach Kenntnis der Daten festgelegt werden.’ Es kommt also darauf an, dass Schüler den Unterschied zwischen inhaltlicher und statistischer Absicherung von Hypothesen erkennen. Soll eine Auffälligkeit statistisch abgesichert werden, so darf dies nicht an den Daten geschehen, an denen die Auffälligkeit erkannt worden ist. Diese klare und einfache Abgrenzung muss im Unterricht deutlich werden, wenn Schüler die ‚Philosophie’ der klassischen Testverfahren und ihrer Anwendungen durchschauen sollen.

 

Literatur

Bruhn, J. (1986): Statistische Verfahren. Braunschweig-Wiesbaden: Vieweg.

Borovcnik, M. (1984): Was bedeuten statistische Aussagen. Wien-Stuttgart: Hölder-Pichler-Tempsky / B.G. Teubner.

Engel, A. (1982): Statistik auf der Schule: Ideen und Beispiele aus neuerer Zeit. In: Der Mathematik-Unterricht 28, 57-85.

Ihm. P. (1980): Explorative und konfirmatorische Datenanalyse — Gegensatz oder Ergänzung? In: N. Victor e.a.(Hrsg.): Explorative Datenanalyse. Berlin-Heidelberg-New York: Springer.

Unkelbach, H.D. und T. Wolf (1983): Ehrlichkeit beim statistischen Testen. In: Vollmar, J. (Hrsg.): Biometrie in der chemisch-pharmazeutischen Industrie. Stuttgart-New York: G. Fischer.

 

Prof. Jörn Bruhn

Institut für Didaktik der Mathematik und Naturwissenschaften

Universität Hamburg

D-2000 Hamburg